The France Cybersecurity Challenge (FCSC) is a CTF organized every year by ANSSI. Here is my write-up of the Windows reverse challenge named Polygraph, including my errors and lessons learned about it.

About FCSC CTF

The France Cybersecurity Challenge (FCSC) is a CTF organized every year by ANSSI. It was clearly not my goal but the FCSC aims to select the best French players to form Team France for the European Cybersecurity Challenge (ECSC).

Polygraph write-up

Here is the challenge description :

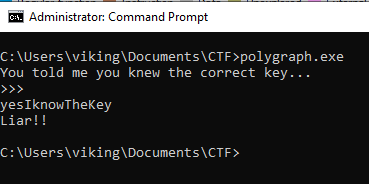
” You told us that you knew the secret. If that is indeed the case, then there will be no problem. Otherwise… “

When you run the polygraph.exe file, it asks for a key then check if the entered key is correct and display “Liar!!” when the key is not correct.

It’s time for decompiling and find a correct key to provide.

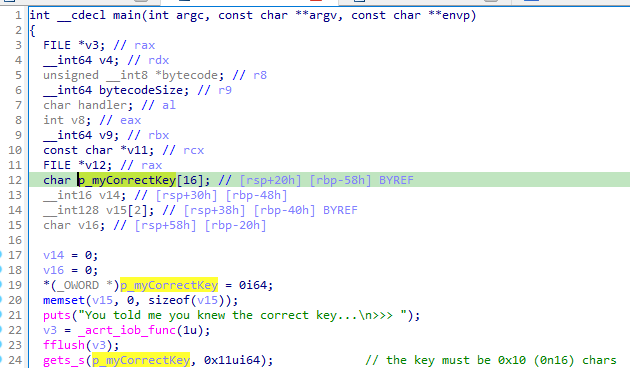
First have a look at the main function. Line 1 to 24 are easy to understand : we can see there is no argument for the program, it just ask for a key using gets_s and store the key in a buffer (with a maximum key size of 16 bytes).

Then the section from line 25 to 28 initializes variables :

• bytecode : VM bytecode stored in memory starting at offset polygraph+0x5041
• registers_5F60 : a 16 bytes variable used to store registers / operations results at offset polygraph+0x5f60
• instructionsCounter : the number of instructions

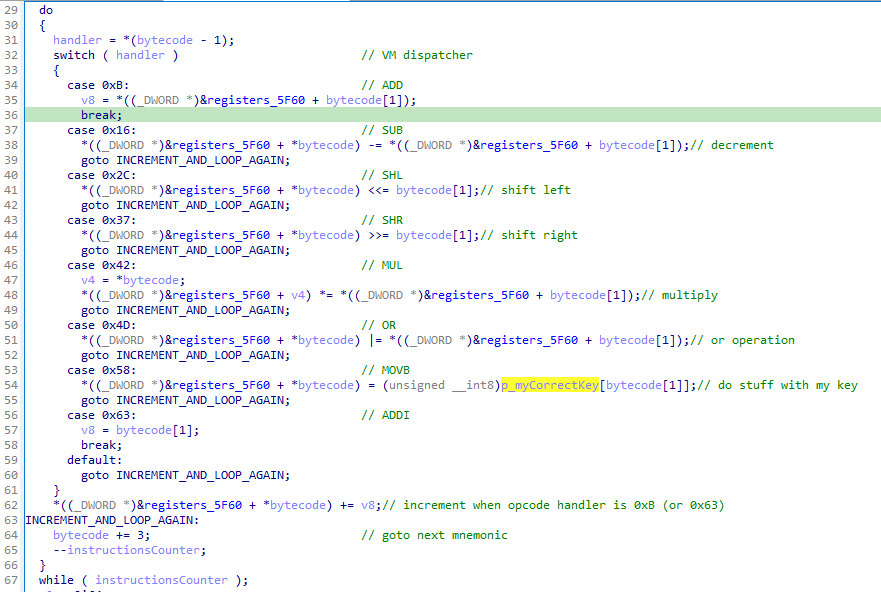
Then from line 29 to 67 this is the block which process the key entered by the user and executing an obfuscation VM bytecode routine. The bytecode is processed 3 bytes (triplets) by 3 bytes where an instruction look like this :

{ byte1, byte2, byte3} : { mnemonic, destination operand, source operand}

Several operations are available : ADD, SUB, SHL, etc.

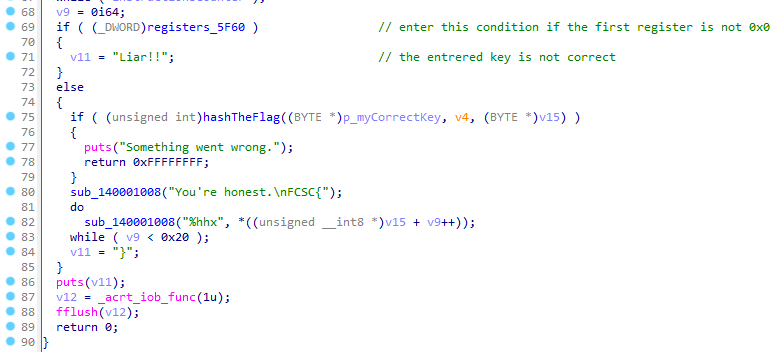
And what about the end of the main function from line 68 to 90 ? After obfuscated VM bytecode run, if the first register position is not equal to zero the challenge displays “Liar” message.

Of course we have to find a way this value be zero !

The end of the code is CTF related : get a hash of the correct key and format the flag to be submitted as FCSC{hashedCorrectKey}

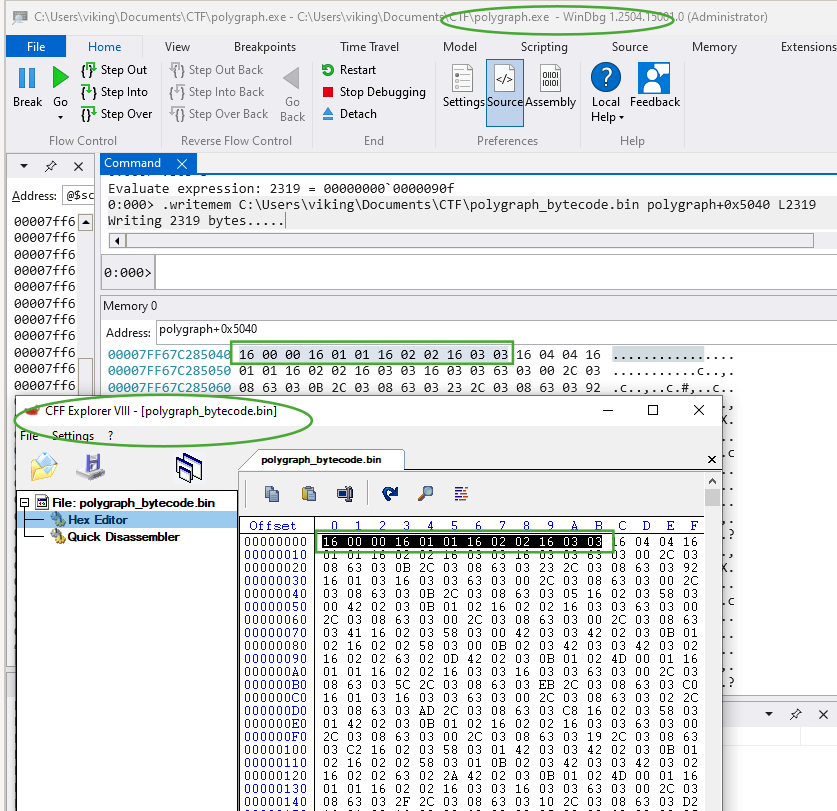
We have to extract the bytecode and to analyze it. Because it contains 0x365 “byte triplets”, we will extract 0x365 * 3 = 2319 bytes starting at offset polygraph+0x5040. Lets’ use Windbg for extracting this payload to polygraph_bytecode.bin file then open with CFF Explorer for double check the extracted bytes are those we expected.

0:000> ?305*3
Evaluate expression: 2319 = 00000000`0000090f

0:000> .writemem C:\Users\viking\Documents\CTF\polygraph_bytecode.bin polygraph+0x5040 L2319
Writing 2319 bytes.....

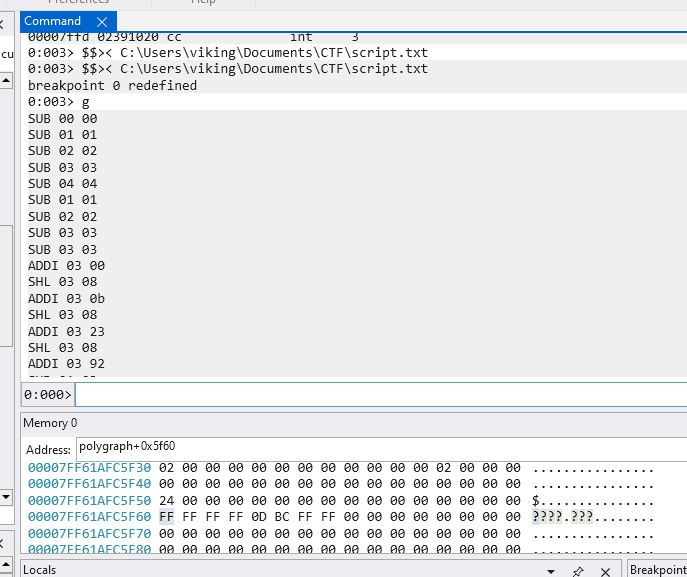
In order to know what this bytecode does I first wrote a windbg script which transform bytes into pseudo-assembly code : my goal was to emulate the VM. The script setup a breakpoint at polygraph+0x11e2 and store byte triplets (discussed above) addresses in 3 variables named $t0 (for the mnemonic), $t1 (for the destination operand) and $t2 (for the source operand). Then it looks at the mnemonic value (for example 0x0B) and displays the corresponding operation (for example 0x0B is the “ADD” operation).

bu polygraph+0x11e2 "r @$t0 = @r8-1; r @$t1 = @r8; r @$t2 = @r8+1; 
.block { 
    .if    (by @$t0 == 0B) {.printf \"ADD %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF;  }
    .elsif (by @$t0 == 16) {.printf \"SUB %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF; } 
    .elsif (by @$t0 == 2C) {.printf \"SHL %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF;}
    .elsif (by @$t0 == 37) {.printf \"SHR %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF;}  
    .elsif (by @$t0 == 42) {.printf \"MUL %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF;}  
    .elsif (by @$t0 == 4D) {.printf \"OR %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF;}  
    .elsif (by @$t0 == 58) {.printf \"MOVB %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF;}  
    .elsif (by @$t0 == 63) {.printf \"ADDI %02x %02x\\n\",poi(@$t1) & 0xFF,poi(@$t2) & 0xFF;}  
    .else {.echo [ERROR_UNKNOWN_MNEMONIC]; db $t0 L1; }
}; "

Then I loaded the script in Windbg using the following command.

$$>< C:\Users\viking\Documents\CTF\script.txt

Note : the purpose of this obscure command line is documented : the $$>< and $>< tokens execute the commands that are found in the script file literally, which means they open the script file, replace all carriage returns with semicolons, and execute the resulting text as a single command block.

I expected emulating those opcodes should make assembly code more readable… and here is the result : not so readable loool

Static reversing can be a complex task if many registers are involved. I was wondering : what is the number of registers used ?

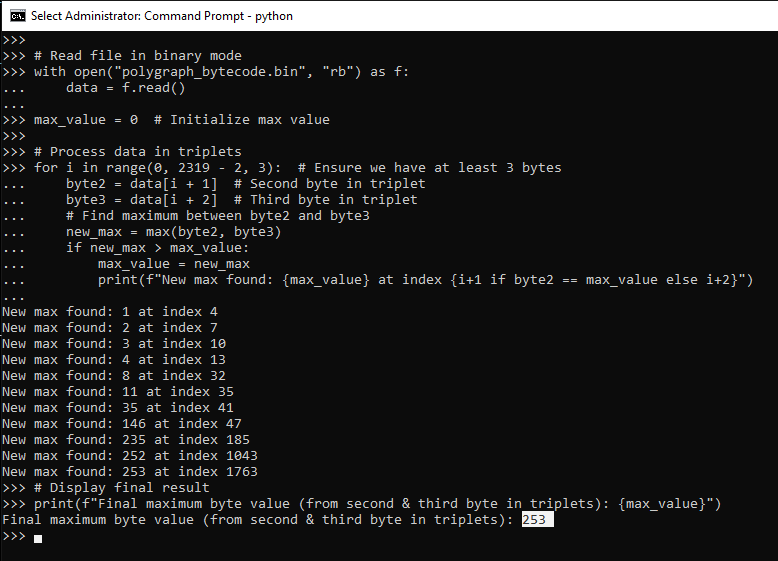
Answering this question implies to find the maximum value for destination operand and source operand, so I followed those steps :

1. read polygraph_bytecode.bin file sequentially

2. for each triplet { mnemonic, destination operand, source operand} evaluate the second and third elements

# Read file in binary mode
with open("polygraph_bytecode.bin", "rb") as f:
    data = f.read()

max_value = 0  # Initialize max value

# Process data in triplets
for i in range(0, 2319 - 2, 3):  # Ensure we have at least 3 bytes
    byte2 = data[i + 1]  # Second byte in triplet
    byte3 = data[i + 2]  # Third byte in triplet
    # Find maximum between byte2 and byte3
    new_max = max(byte2, byte3)
    if new_max > max_value:
        max_value = new_max
        print(f"New max found: {max_value} at index {i+1 if byte2 == max_value else i+2}")

# Display final result
print(f"Final maximum byte value (from second & third byte in triplets): {max_value}")

And here the result :

Woow when I saw there is a potential of 253 registers that can be used I wonder how the assembly code could be analyzed easily ?

Well a colleague of mine (thanks @WooT :-)) told me that VM obfuscation is a classic when doing CTF Reverse tasks : ok, thing I learned :-)

In order to solve this challenge I have to use SMT solver but what is this ? Here is a quick explanation from MS Copilot which is pretty clear :

An SMT (Satisfiability Modulo Theories) solver helps analyze and solve complex logical constraints. When dealing with obfuscated VM bytecode, 
it's used to reverse-engineer how the virtual machine executes instructions by symbolically evaluating conditions and variables. 
Essentially, it helps break down the obfuscation and determine the underlying logic of the bytecode, making it easier to understand or deobfuscate. 
Let's say we have an obfuscated VM that performs some mysterious arithmetic operations on a given input. Instead of executing the bytecode directly, 
we use an SMT solver to model the VM's behavior symbolically.

Here's a simplified example:
- The VM takes an input x and transforms it using hidden rules.
- Instead of trying every possible x, we define symbolic variables (x, y, z) representing unknown values.
- The SMT solver translates the VM's logic into mathematical constraints.
- Then, it finds values of x, y, and z that satisfy those constraints.
This allows us to extract hidden logic without brute-force testing each possibility, making the deobfuscation process much more efficient.

But what are the steps to follow ? I found this video very useful : Introduction to the Z3 Solver framework with the Hex-Rays CTF Challenge 2023.

Here is the plan for solving this challenge :

step 1 - use 3 global variables for :

• storing the key entered by the user
• storing the registers used when VM bytecode runs
• setup a Z3 solver instance

userkey    = [z3.BitVec(f"k{i}", 8) for i in range(16)]
registers    = [z3.BitVec(f"r{i}", 32) for i in range(getRegisters())]
solver = z3.Solver()

step 2 - load VM bytecode from file and emulate all operations

    instructionsCounter = 2319
    with open("polygraph_bytecode.bin", "rb") as f:
        while instructionsCounter >= 3:
            chunk = f.read(3)
            if len(chunk) < 3:
                break  # Stop at end of file

            # Unpack 3 bytes as unsigned integers
            operation_Opcode, dest, src = struct.unpack("BBB", chunk)

            # Operations on registers
            if   operation_Opcode == 0x0B: registers[dest] = to_dword(registers[dest] + registers[src])     
            elif operation_Opcode == 0x16: registers[dest] = to_dword(registers[dest] - registers[src])     
            elif operation_Opcode == 0x2C: registers[dest] = to_dword(registers[dest] << src)               
            elif operation_Opcode == 0x37: registers[dest] = to_dword(registers[dest] >> src)               
            elif operation_Opcode == 0x42: registers[dest] = to_dword(registers[dest] * registers[src])     
            elif operation_Opcode == 0x4D: registers[dest] = to_dword(registers[dest] | registers[src])     
            elif operation_Opcode == 0x58: registers[dest] = to_dword(z3.ZeroExt(24, userkey[src & 0x0F]))  
            elif operation_Opcode == 0x63: registers[dest] = to_dword(registers[dest] + src)                
            else:
                break

            instructionsCounter -= 3  # Decrement the counter

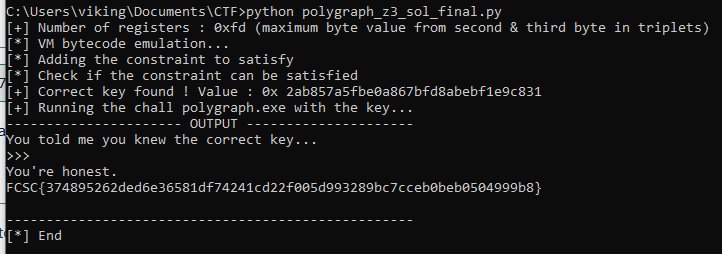
step 3 - add the constraint to solve : as shown previously the first register byte must be 0x0

    solver.add(registers[0] == 0)

step 4 - use the Z3 SMT solver for getting the constraint satisfied

    if solver.check() == z3.sat:
        model = solver.model() # retrieves the concrete values that satisfy the constraints
        correctKey_bytes = bytes([model.evaluate(k).as_long() for k in userkey])
        print("[+] Correct key found ! Value : 0x", correctKey_bytes.hex())

step 5 - enjoy the flag

Lessons learned

A CTF is an opportunity to learn new techniques, and here are the lessons I drew from it :

• VM obfuscation is a classic when doing CTF Reverse tasks

• Z3 SMT solver does the job perfectly

Thanks for reading, I hope you learnt something and your feedbacks are welcome !

The full PoC code is commented and available below.

#!/usr/bin/env python3
import sys, struct, z3, subprocess
from pathlib import Path

def getRegisters():
    # Read file in binary mode
    with open("polygraph_bytecode.bin", "rb") as f:
        data = f.read()

    max_value = 0  # Initialize max value

    # Process data in triplets
    for i in range(0, 2319 - 2, 3):  # Ensure we have at least 3 bytes
        byte2 = data[i + 1]  # Second byte in triplet
        byte3 = data[i + 2]  # Third byte in triplet
        # Find maximum between byte2 and byte3
        new_max = max(byte2, byte3)
        if new_max > max_value:
            max_value = new_max
            #print(f"[*] New max found: {hex(max_value)} at index {i+1 if byte2 == max_value else i+2}")

    # Display final result
    print(f"[+] Number of registers : {hex(max_value)} (maximum byte value from second & third byte in triplets)")
    return max_value

# Extracts bits 31 down to 0 from expr (i.e., a 32-bit value).
# The result is a new bit-vector containing only these selected bits.
# This is equivalent to masking the lower 32 bits while ignoring higher bits.
def to_dword(expr):
    return z3.Extract(31, 0, expr)

# Global variables
userkey    = [z3.BitVec(f"k{i}", 8) for i in range(16)]
registers    = [z3.BitVec(f"r{i}", 32) for i in range(getRegisters())]
solver = z3.Solver()

def main():
    print("[*] VM bytecode emulation...")
    # Open file in binary mode and iterate over triplets
    instructionsCounter = 2319
    with open("polygraph_bytecode.bin", "rb") as f:
        while instructionsCounter >= 3:
            chunk = f.read(3)
            if len(chunk) < 3:
                break  # Stop at end of file

            # Unpack 3 bytes as unsigned integers
            operation_Opcode, dest, src = struct.unpack("BBB", chunk)
            if   operation_Opcode == 0x0B: registers[dest] = to_dword(registers[dest] + registers[src])     # *((_DWORD *)&registers_5F60 + *bytecode) += *((_DWORD *)&registers_5F60 + bytecode[1])
            elif operation_Opcode == 0x16: registers[dest] = to_dword(registers[dest] - registers[src])     # *((_DWORD *)&registers_5F60 + *bytecode) -= *((_DWORD *)&registers_5F60 + bytecode[1])
            elif operation_Opcode == 0x2C: registers[dest] = to_dword(registers[dest] << src)               # *((_DWORD *)&registers_5F60 + *bytecode) <<= bytecode[1]
            elif operation_Opcode == 0x37: registers[dest] = to_dword(registers[dest] >> src)               # *((_DWORD *)&registers_5F60 + *bytecode) >>= bytecode[1]
            elif operation_Opcode == 0x42: registers[dest] = to_dword(registers[dest] * registers[src])     # *((_DWORD *)&registers_5F60 + *bytecode) *= *((_DWORD *)&registers_5F60 + bytecode[1])
            elif operation_Opcode == 0x4D: registers[dest] = to_dword(registers[dest] | registers[src])     # *((_DWORD *)&registers_5F60 + *bytecode) |= *((_DWORD *)&registers_5F60 + bytecode[1])
            elif operation_Opcode == 0x58: registers[dest] = to_dword(z3.ZeroExt(24, userkey[src & 0x0F]))  # *((_DWORD *)&registers_5F60 + *bytecode) = (unsigned __int8)p_myCorrectKey[bytecode[1]]
                                                                                                            # Extends userkey[src & 0x0F] from 8 bits to 32 bits. Fills higher 24 bits with zeros, preserving unsigned representation.
            elif operation_Opcode == 0x63: registers[dest] = to_dword(registers[dest] + src)                # *((_DWORD *)&registers_5F60 + *bytecode) += bytecode[1]
            else:
                break

            instructionsCounter -= 3  # Decrement the counter

    print("[*] Adding the constraint to satisfy")
    solver.add(registers[0] == 0)

    print("[*] Check if the constraint can be satisfied")
    if solver.check() == z3.sat:
        model = solver.model() # retrieves the concrete values that satisfy the constraints
        correctKey_bytes = bytes([model.evaluate(k).as_long() for k in userkey])
        print("[+] Correct key found ! Value : 0x", correctKey_bytes.hex())
        print("[+] Running the chall polygraph.exe with the key...")
        print("---------------------- OUTPUT ---------------------")
        process = subprocess.run(["polygraph.exe"], input=correctKey_bytes, capture_output=True)
        print(process.stdout.decode())  # Convert bytes to string and print normally
        print("---------------------------------------------------")
    else:
        print("[-] No solution found")
    
    print("[*] End")

#
# START THE MAIN
#
if __name__ == "__main__":
    main()

Resources :

All things IDA (Youtube channel) - Introduction to the Z3 Solver framework with the Hex-Rays CTF Challenge 2023
synthesis.to - Writing Disassemblers for VM-based Obfuscators
FCSC website - https://fcsc.fr/
FCSC polygraph - https://hackropole.fr/en/challenges/reverse/fcsc2025-reverse-polygraph/